
Conhecendo as Ondas Hertzianas
| NAVEGUE NAS ONDAS CURTAS DO RÁDIO | ARTIGOS TÉCNICOS DX | ENVIE SEUS COMENTÁRIOS | PROCURE NESTE SÍTIO |
 |
Conhecendo as Ondas Hertzianas |
ONDAS
A transmissão de rádio é feita por meio de ondas. A palavra onda nos faz lembrar a onda de água de um lago. Se nós atirarmos uma pedra na superfície do lago, logo notamos a formação de ondas circulares em volta do local onde caiu a pedra. Vamos imaginar o corte da superfície do lago; poderemos visualizar como se formam as ondas. Na figura abaixo, podemos observar o movimento de um hipotético cilindro de cortiça a flutuar no centro da onda.

Observando o ponto em que a pedra caiu na superfície da água, notaremos uma formação de sucessivas ondas que se deslocam afastando-se do ponto de origem. A onda sofre um amortecimento gradativo à medida que se afasta do ponto inicial, devido à resistência encontrada pela água. Se colocarmos um barquinho de papel sobre a onda, notaremos que a onda o fará saltar deixando-o, porém, no mesmo lugar; isto é, o barquinho de papel não se desloca com o movimento da onda na superfície do lago.
Então, o que é que se desloca numa onda ? Fazendo analogia ao ato de se enfileirar pedras de dominó de forma vertical e uniformemente espaçadas umas das outras, ao se empurrar a primeira pedra da seqüência, a um efeito em cadeia onde cada uma empurra a seguinte, derrubando toda a serie. O movimento, ou onda, passa por toda a serie de pedras e poderemos verificar que as pedras do dominó permanecem praticamente no mesmo lugar original. O mesmo fenômeno ocorre com a onda formada no lago.
Portanto, podemos dizer que a energia aplicada à primeira pedra se desloca em todas as pedras enfileiradas até a ultima pedra do dominó. Portanto, no exemplo da onda do lago, não são as partículas de água que se deslocam sobre a superfície do lago, mas sim a energia. A água e as pedras do domino utilizadas como exemplos são os meios onde a energia se propaga.
Podemos definir as ondas como "Perturbação do meio caracterizada pelo transporte de energia e quantidade de movimento, sem o transporte de matéria." Também, podemos classificar as ondas conforme suas duas naturezas :
1- Ondas
eletromagnéticas -
produzidas pela vibração de cargas elétricas
(não necessita de meio material para se propagar).
2- Ondas mecânicas
- oscilações de um meio elástico, portanto necessitam de
meio material para existir.
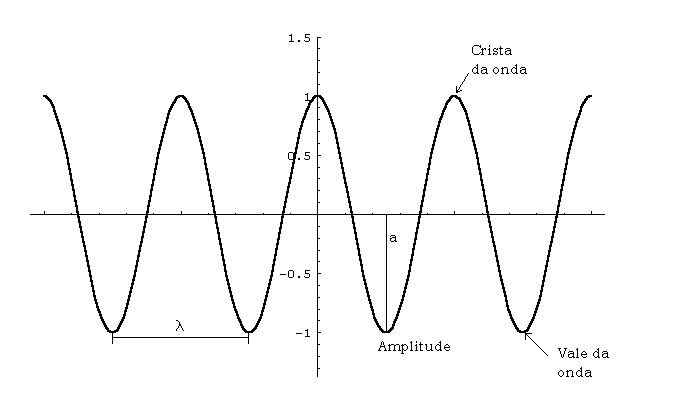
As características da onda são mostradas abaixo.
 |
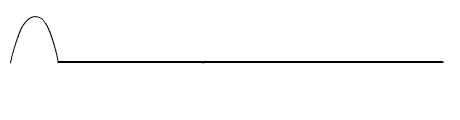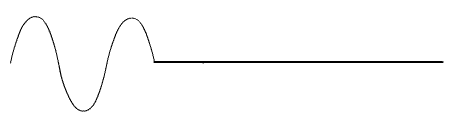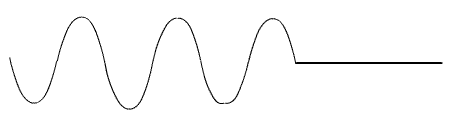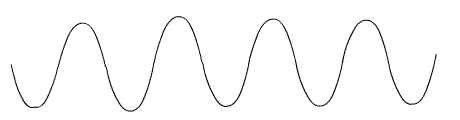 |
A diferença da parte mais baixa até a parte mais alta da onda é chamada de amplitude da onda. A parte mais alta da onda podemos chamar de crista ou pico da onda. A distancia entre duas cristas ou picos consecutivos é o que chamamos de comprimento da onda. Ao trajeto percorrido para realizar um comprimento de uma onda chamamos de ciclo. O numero de ciclos completados na unidade do tempo de um segundo chamamos de freqüência.
ONDAS ELETROMAGNÉTICAS
A radiocomunicação também se faz através da propagação da energia pelas ondas, no caso pela onda eletromagnética. O que é uma onda eletromagnética ?
A onda eletromagnética compreende uma ampla variedade de ondas : ondas sonoras, ondas de calor, ondas luminosas, ondas Hertzianas ( conhecidas como ondas de radio freqüência e vulgarmente como ondas de radio ), ondas de raios X e diversas outras ondas.
Para entender o conceito, é importante conhecer um breve histórico do desenvolvimento da eletricidade e do magnetismo. Na primeira metade do século XIX era conhecido que fios transmitindo correntes elétricas produziam um campo de indução ao redor do fio, o qual é capaz de causar ações sobre curtas distancias. Também era conhecido que este campo de indução é um campo magnético, e este conhecimento formou a base para os motores elétricos. Em 1887, o físico alemão Heinrich Hertz demonstrou que sinais de radio são ondas eletromagnéticas, que nem a luz. Assim como o campo de indução, a onda eletromagnética é criada por uma corrente elétrica movendo em um condutos ( ex. fio de cobre ). Diferente do campo de indução entretanto, o campo irradiado sai do condutor e se propaga através do espaço como uma onda eletromagnética.
Como já demonstrado na analogia das ondas na água, existem duas propriedade relacionadas a todas as ondas que são muito importantes as ondas de radio também : freqüência ( f ) e comprimento de onda ( λ ). A freqüência é o numero de oscilações ( ou ciclos ) por unidade de tempo. Nas ondas de radio, a unidade de tempo utilizada é o segundo, logo, a freqüência é uma expressão do numero de ciclos por segundo ( cps ). Se o período de tempo necessário para a onda se deslocar do ponto A para o B é um segundo ( 1 s ), e existem dois ciclos completos neste espaço, então a freqüência da onda criada é 2 cps.
No inicio, as freqüência de radio ( assim como as freqüência de outras ondas elétricas e acústicas ) eram expressadas em cps, mas em honra ao físico Heirich Hertz, a unidade foi renomeada para Hertz ( Hz ) muitos anos atrás. Devido as unidades serem iguais ( 1 Hz = 1 cps ), a onda imaginária no nosso exemplo tem freqüência de 2 Hz.
Devido as freqüências de radio serem altas, a freqüência é geralmente expressa em kilohertz ( kHz - 1000s de Hz ) e megahertz ( MHz - 1.000.000s de Hz ). Logo, a freqüência de uma estação operando no meio da banda de radiodifusão AM pode ser expressa como 1.000.000 Hz, ou 1000 kHz ou 1 MHz, todos equivalentes entre si.
Os dials ( mostradores de freqüência dos receptores ) fabricados nos Eua são normalmente calibrados em kHz ou MHz. Na Europa e em algumas outras partes do mundo, por outro lado, não é raro encontrar dials calibrados em metros, a unidade do comprimento de onda, assim como a freqüência.
O comprimento de onda de qualquer onda é a distancia entre os picos da forma de onda. Podemos também medir a mesma distancia entre sucessivos picos negativos ( inferiores ), ou entre duas características similares em ondas sucessivas. Em radio, o comprimento de onda do sinal é expresso em metros. O comprimento de onda é proporcional ao inverso da freqüência. O comprimento de onda de qualquer onda é relacionado a freqüência logo : fλ = v , onde f é a freqüência em Hz, λ é o comprimento de onda em metros, e v é a velocidade da propagação em metros por segundo ( m/s ). Devido às ondas de radio propagaram a velocidade da luz ( o que é naturalmente também uma onda eletromagnética ) - aproximadamente 300.000.000 m/s tanto no espaço livre e na atmosfera - a letra minúscula c é usada para representar a velocidade ( ao invés de v ). Assim, podemos reescrever esta expressão na forma :
fHz = c / λmetros = 300.000.000 / λmetros
Podemos simplificar e abreviar utilizando as unidades kHz e MHz :
FkHz = 300.000 / λmetros
fMHz = 300 / λmetros
Utilizando as expressões acima, podemos calcular o comprimento de onda para diversas freqüências diferentes como exemplo : 100 kHz, 1 MHz ( na banda de Ondas Medias ), 10 MHz ( já nas Ondas Curtas ), e 1000 MHz ( faixa de microondas ). São respectivamente 3000 m ( 100 kHz ), 300 m ( 1 MHz ), 30 m ( 10 MHz ) e 0.3 m, ou 30 cm ( 1000 MHz ).
Você pode ver a partir destes números o porque de 1 MHz estar dentro do que chamados de faixa de ondas médias, 10 MHz está dentro da faixa de ondas curtas e 1000 MHz está dentro das microondas ( onda "muito pequena" ).
Abaixo está representado o espectro de Radio Freqüência que compreende de 30 kHz até 300 GigaHertz conforme normatizado pelo ITU - International Telecommunications Union.
|
N° da Banda |
Símbolo |
Intervalo de Frequencia (limite inferior exclusivo,limite superior inclusivo) |
Subdivisão métrica correspondente |
Abreviações métricas para as bandas |
|
3 |
ULF |
300 - 3000 kHz |
Hectokilometrica |
B.hkm |
|
4 |
VLF |
3 - 30 kHz |
Myriametrica |
B.Mam |
|
5 |
LF |
30 - 300 kHz |
Kilometrica |
B.km |
|
6 |
MF |
300 - 3000 kHz |
Hectometrica |
B.hm |
|
7 |
HF |
3 - 30 MHz |
Decametrica |
B.dam |
|
8 |
VHF |
30 - 300 MHz |
Metrica |
B.m |
|
9 |
UHF |
300 - 3000 MHz |
Decimetrica |
B.dm |
|
10 |
SHF |
3 - 30 GHz |
Centimetrica |
B.cm |
|
11 |
EHF |
30 - 300 GHz |
Millimetrica |
B.mm |
|
12 |
300 - 3000 GHz |
Decimillimetrica |
B.dmm |
|
|
13 |
3 - 30 THz |
Centimillimetrica |
B.cmm |
|
|
14 |
30 - 300 THz |
Micrometrica |
B.mm |
|
|
15 |
300 - 3000 THz |
Decimicrometrica |
B.dmm |
Unidades :
k: kilo (103),
M: mega (106),
G: giga (109),
T: tera (1012);
m: micro
(10–6),
m: milli (10–3),
c: centi (10–2),
d: deci (10–1);
da: deca (10), h: hecto (102),
Ma: myria (104).
Na tabela abaixo estão representadas as faixas de freqüência de rádio e suas denominações.
| Onda | Freqüência | Faixa | Em português |
| Som | 15 kHz | Ultra Som até 20 kHz | |
| VLF | 30 kHz | Very Low Frequency | Freqüência Muito Baixa |
| LF | 300 kHz | Low Frequency | Baixa Freqüência ( Ondas Londas ) |
| MF | 3 MHz | Medium Frequency | Media Freqüência ( Ondas Médias ) |
| HF | 30 MHz | High Frequency | Alta Freqüência ( Ondas Curtas ) |
| VHF | 300 MHz | Very Figh Frequency | Muito Alta Freqüência |
| UHF | 3 GHz | Ultra High Frequency | Ultra Alta Freqüência |
| SHF | 30 GHz | Super High Frequency | Super Alta Freqüência |
| EHF | 300 GHz | Extremely High Frequency | Extremamente Alta Freqüência |
| Infra Vermelho | |||
| Luz visível | |||
| Ultra Violeta | |||
| Raios X | |||
| Raios Gama |
A diferença entre um tipo de onda e outro está no comprimento ( e na freqüência ) que esta onda apresenta, ambas resultantes do meio em que ela se propaga e da fonte que a gerou. Todavia, para nossa finalidade de transmissão e recepção de ondas de radio, o que mais nos interessa no espectro das ondas eletromagnéticas são as ondas Hertzianas.
CAMPO ELETROMAGNÉTICO - BREVE VISÃO
Para se ter uma compreensão clara das interações dos campos elétricos e magnéticos que compõem as ondas "eletromagnéticas", seria necessário analisar com profundidade as famosas equações da luz de Maxwell. Porém, apenas para ilustrar como as ondas são formadas, é importante mostrar que as ondas de radio apresentam freqüência muito menor que a da luz, infravermelho, ultra violeta e etc. A onda eletromagnética consiste de dois campos oscilantes mutuamente perpendiculares, viajando junto em fase. Um dos campos é um campo elétrico e o outro é o campo magnético.
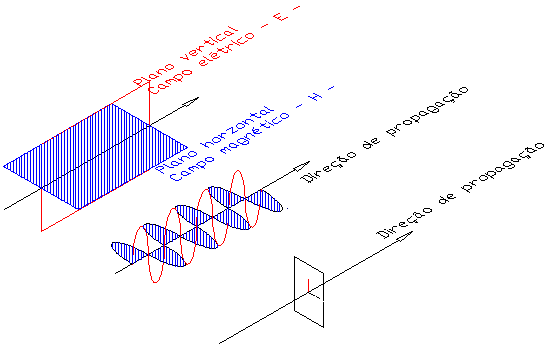
E - Campo Elétrico
H - Campo Magnético
INTENSIDADE DA ONDA DE RADIO
A onda de rádio é atenuada ( reduzida em potencia aparente ) conforme se propaga do transmissor até o receptor. Mesmo que em freqüências muito altas de microondas, existem perdas adicionais como resultado do conteúdo de oxigênio e vapor de água existente no ar. Em outras freqüências outras perdas existem. As ondas de radio de todas as freqüências sofrem perdas devida a lei do quadrado inverso. Vamos dar uma olhada neste fenômeno.
O vetor campo elétrico se desvanece em proporção direta a distancia percorrida. O campo E é medido em termos de Volts por metro ( V/m ), ou em subunidade milivolt por metro ( mV/m ) ou microvolt por metro ( uV/m ). Isto significa, se um campo E de 10 V/m cruza seu corpo da cabeça aos pés, e você mede 2 metros de altura, então uma tensão elétrica é gerada de ( 2m ) x ( 10 V/m ), ou 20 Volts. A redução do campo E é linearmente relacionada a distancia ( ex. se a distancia dobra a tensão do campo E cai a metade ). Logo, um campo E de 100 mV/m medido a 1 kilometro do transmissor será 50 mV/m em 2 kilometros.
A energia em qualquer sistema elétrico é relacionada a tensão ( voltagem ) através da relação :
P = E2 / R
onde
P é
a energia em Watts ( W )
R é a resistência em Ohms ( Ω )
E é o potencial elétrico em Volts ( V )
No caso de onda de radio, o termo R é substituído pela impedância ( Z ) do espaço livre, que é da ordem de 377 Ohms. Se a intensidade do campo E é, por exemplo, 10 V/m, então a densidade de energia do sinal é :
P = ( 10 V/m )2 / 377 = 0.265 W/m2 = 26.5 mW/m2
A densidade de energia, medida em Watts por metro quadrado, ou as subunidades ( ex. mW/cm2 ), se atenuam com o quadrado da distancia. Este fenômeno pode ser demonstrado graficamente.
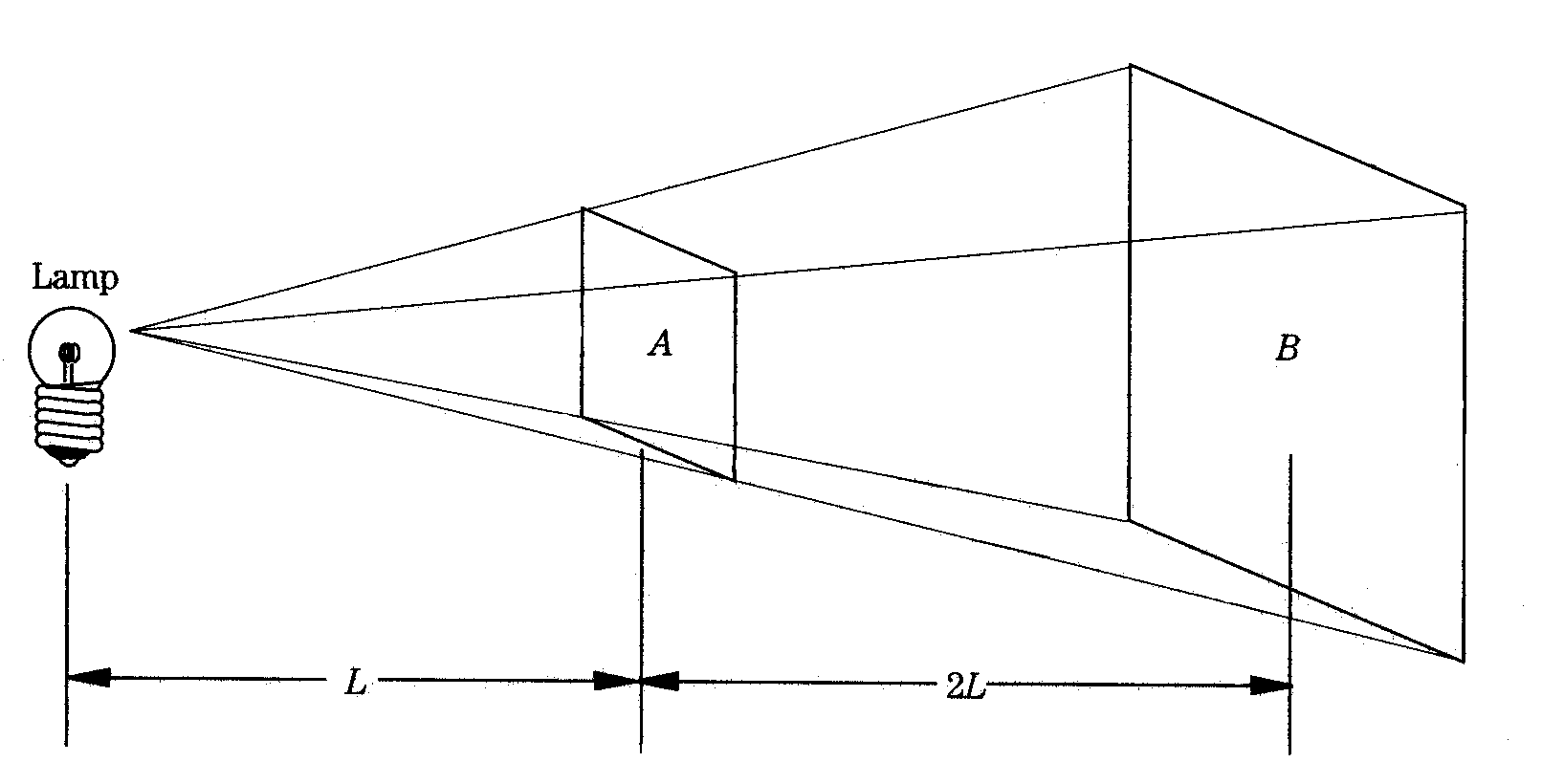
Aqui, você pode ver uma lâmpada emitindo um feixe de luz que ilumina uma superfície (A), a uma distancia (L), com determinada intensidade. Em outra superfície (B), que é 2 vezes a distancia da fonte (2L), a mesma quantidade de energia é distribuída sobre a área (B) que é o dobro do tamanho da área (A). Assim, a intensidade da energia cai conforme a equação 1/d2 , onde d é a distancia.
Isto é chamado a lei do quadrado inverso.
Fontes
ITU - International
Telecommunicatuions Union
Practical Antena Handbook - Joseph Carr - McGraw Hill
The ARRL Handbook 2002 - ARRL
Electromagnetic Waves and Radiatins Systems - Jordan - Prentice Hall
 |
Retorna para o Guia de Navegação |
|
Sitio dedicado ao Rádio
de Ondas Curtas e a prática DX -
Navegue nas Ondas Curtas do Rádio |
Acessos desde 2002